Методы решения квадратных уравнений

Корней нет

D = 0

D 0

13.11.18

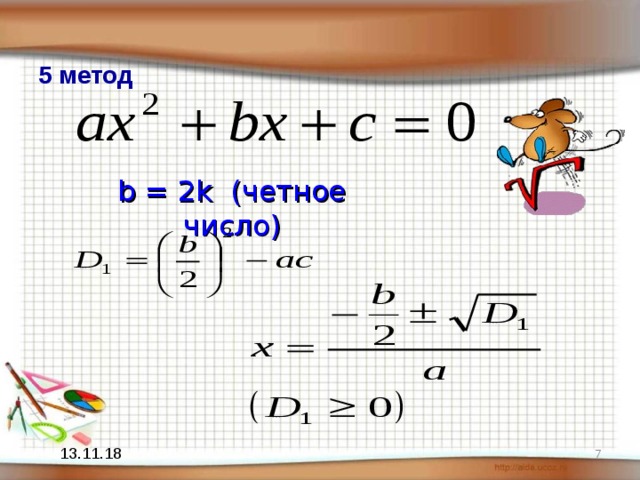
5 метод

b = 2k ( четное число)

13.11.18

Теорема Виета

6 метод

x 1 и х 2 – корни уравнения

x 1 и х 2 – корни уравнения

13.11.18

Работа с карточкой

Уравнение

a

x 2 — 7 x + 12 = 0

b

c

5

5 x 2 = 15 x

b 2 — 4ac

— 7

x 1

-6

3

x 2

0

x 1 + x 2

-75

x 1 · x 2

13.11.18

Работа с карточкой

Уравнение

a

x 2 — 7 x + 12 = 0

b

5 x 2 — 7 x — 6 = 0

1

c

5

5 x 2 = 15 x

-7

b 2 — 4ac

5

— 7

12

3 x 2 — 75 = 0

x 1

1

-15

3

-6

x 2

0

0

169

4

x 1 + x 2

2

-75

3

225

x 1 · x 2

7

0

-0,6

900

1,4

5

12

3

-5

3

-1,2

0

0

-25

13.11.18

Специальные методы:

• Метод выделения квадрата двучлена.
• Метод «переброски» старшего коэффициента
• На основании теорем:

13.11.18

Метод выделения квадрата двучлена.

7 метод

Цель: привести квадратное уравнение общего вида к неполному квадратному уравнению.

Пример:

a 2 +2ab+b 2 =(a + b) 2 a 2 -b 2 =(a-b)(a + b)

13.11.18

Метод выделения квадрата двучлена.

Пример: х 2 + 6х – 7 = 0

Выделим в левой части полный квадрат.

Запишем выражение х 2 + 6х в следующем виде: х 2 + 6х = х 2 + 2· х ·3,

чтобы получить полный квадрат, нужно прибавить 3 2 , так как

х 2 + 2· х ·3 + 3 2 = (х + 3) 2 .

Преобразуем теперь левую часть уравнения х 2 + 6х – 7 = 0 , прибавляя

к ней и вычитая 3 2. Имеем:

х 2 + 6х – 7 = х 2 + 2· х ·3 + 3 2 – 3 2 – 7 = (х + 3) 2 – 9 – 7 = (х + 3) 2 – 16.

Таким образом, данное уравнение можно записать так:

(х + 3) 2 –16 = 0 , т.е. (х + 3) 2 = 16.

Следовательно, х +3 = 4, или х +3 = — 4 ,

х 1 = 1, х 2 = – 7.

13.11.18

Метод «переброски» старшего коэффициента.

8 метод

Корни квадратных уравнений

и

связаны соотношениями

и

В некоторых случаях бывает удобно решать сначала не данное квадратное уравнение, а приведенное, полученное «переброской» коэффициента а .

Пример:

= = Х 2 = 2,5 У 1 * У 2 = 30 У 2 = 5 Х 2 = Ответ : 3 и 2,5″ width=»640″

Метод «переброски» старшего коэффициента.

Пример:

«Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

у 2 – 11 y +30 = 0.

Согласно теореме Виета

У 1 +У 2 =11 У 1 =6 Х 1 =

Х 1 =3

=

=

=

Х 2 = 2,5

У 1 * У 2 = 30 У 2 = 5 Х 2 =

Ответ : 3 и 2,5

На основании теорем:

9 метод

• Если в квадратном уравнении a+b+c=0 , то один из корней равен 1, а

второй по теореме Виета равен

10 метод

• Если в квадратном уравнении a+c=b , то один из корней равен -1,

а второй по теореме Виета равен

Примеры :

На основании теорем:

Примеры :

Решение.

Так как а + b + с = 0 ( 345 – 137 – 208 = 0 ), то х 1 = 1, х 2 =

.

Ответ : 1 ; –

Решение.

Так как а- b +с = 0 ( 132 – 247 +115=0 ), то х 1 = — 1, х 2 = —

Ответ: — 1; —

Общие методы:

• Разложение на множители;
• Введение новой переменной;
• Графический метод .

13.11.18

Метод разложения на множители

11 метод

Цель:

привести квадратное уравнение общего вида к виду

А(х) · В(х)=0,

где А(х) и В(х) – многочлены относительно х.

Способы:

• Вынесение общего множителя за скобки;
• Использование формул сокращенного умножения ;
• Способ группировки.

Пример :

х 2 + 10х – 24 = 0

13.11.18

Метод разложения на множители

х 2 + 10х – 24 = 0

Пример :

Разложим левую часть уравнения на множители:

х 2 + 10х – 24 = х 2 + 12х – 2х – 24 = х (х + 12) – 2 (х +12) = = (х + 12)(х – 2).

Следовательно, уравнение можно переписать так:

(х + 12)(х – 2) = 0.

Так как произведение равно нулю, то по крайне мере один из его множителей равен нулю.

Поэтому левая часть уравнения обращается в нуль при х = 2,

а также при х = — 12 .

Это означает, что 2 и – 12 являются корнями уравнения х 2 + 10х – 24 = 0.

13.11.18

Введение новой переменной .

12 метод

Умение удачно ввести новую переменную – важный элемент математической культуры. Удачный выбор новой переменной делает структуру уравнения более прозрачной.

Пример :

13.11.18

0) по теореме, обратной теореме Виета t 1 + t 2 =3 t 1 * t 2 =2 t 1 = 1, t 2 = 2 Произведем обратную замену и вернемся к переменной х Если t = 1 , то 5х+3=1 Если t = 2, то 5х+3=2 5х=1-3 5х=2-3 5х=-2 5х=-1 Х=-0,4 Х=-0,2 Ответ: -0,4; -0,2 13.11.18″ width=»640″

Введение новой переменной .

Пример :

Пусть: t = 5х + 3 Произведем замену переменной t 2 =3 t -2

Тогда t 2 -3 t +2=0

(Устно проверим условие D 0) по теореме, обратной теореме Виета

t 1 + t 2 =3

t 1 * t 2 =2 t 1 = 1, t 2 = 2

Произведем обратную замену и вернемся к переменной х

Если t = 1 , то 5х+3=1 Если t = 2, то 5х+3=2

5х=1-3 5х=2-3

5х=-2 5х=-1

Х=-0,4 Х=-0,2

Ответ: -0,4; -0,2

13.11.18

Графический метод.

13 метод

Для решения уравнения f ( x ) = g ( x ) необходимо построить графики функций y = f ( x ), y = g ( x ) и найти точки их пересечения; абсциссы точек пересечения и будут корнями уравнения. Замечание : Графический метод часто применяют не для нахождения корней уравнения, а для определения их количества.

Пример: Х 2 -2х-3=0

13.11.18

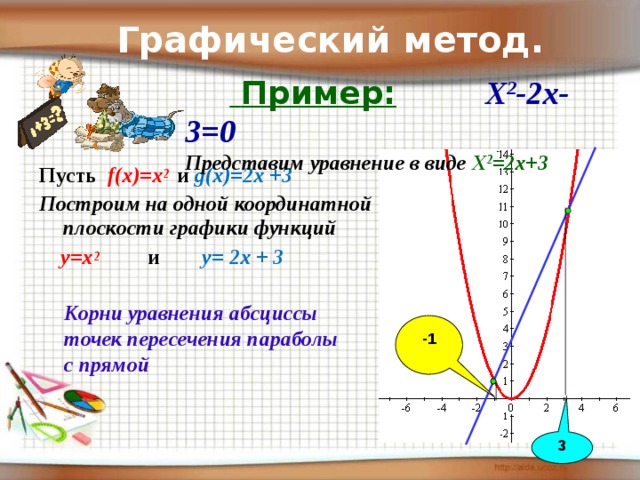
Графический метод.

Пример: Х 2 -2х-3=0 Представим уравнение в виде Х 2 =2х+3

Пусть f(x)=x 2 и g(x)=2x +3

Построим на одной координатной плоскости графики функций

y=x 2 и y= 2x + 3

Корни уравнения абсциссы точек пересечения параболы с прямой

-1

3

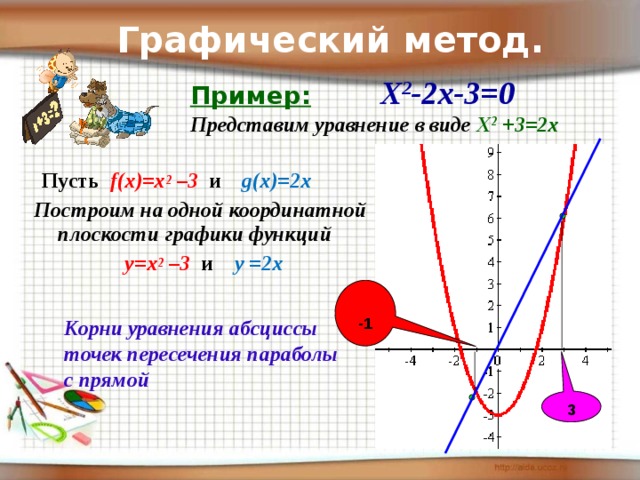
Графический метод.

Пример: Х 2 -2х-3=0 Представим уравнение в виде Х 2 +3=2х

Пусть f(x)=x 2 –3 и g(x)=2x

Построим на одной координатной плоскости графики функций

y=x 2 –3 и y =2x

-1

Корни уравнения абсциссы точек пересечения параболы с прямой

3

«Золотые мысли»

Расставьте номера методов решения уравнений и расшифруйте высказывание

№ / №

Уравнение

1

№ метода

20 x 2 — 6x = 0

2

3x 2 — 5x + 4 = 0

3

100x 2 + 53x – 153 = 0

4

35x 2 – 8 = 0

5

7x 2 + 8x + 2 = 0

6

299x 2 + 300x + 1 = 0

7

4x 2 – 4x + 3 = 0

8

(x – 2 – (3x + 1) 2 = 0

9

4(x – 1) 2 + 0,5(x – 1) – 1 = 0

10

12x 2 = 0

13.11.18

«Золотые мысли»

Расставьте номера методов решения уравнений и расшифруйте высказывание

№ / №

Уравнение

1

№ метода

20 x 2 — 6x = 0

2

3x 2 — 5x + 4 = 0

3

2

4

100x 2 + 53x – 153 = 0

4

35x 2 – 8 = 0

9

5

3

7x 2 + 8x + 2 = 0

6

299x 2 + 300x + 1 = 0

5

7

4x 2 – 4x + 3 = 0

8

10

(x – 2 – (3x + 1) 2 = 0

7

9

11

4(x – 1) 2 + 0,5(x – 1) – 1 = 0

10

12x 2 = 0

12

1

13.11.18

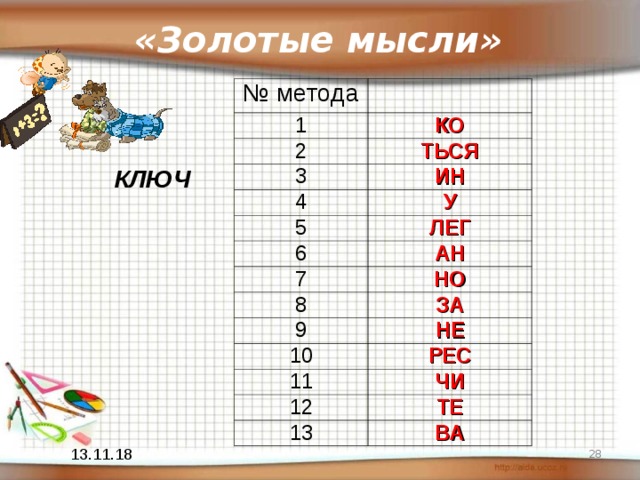
«Золотые мысли»

№ метода

1

КО

2

ТЬСЯ

3

ИН

4

У

5

6

ЛЕГ

7

АН

НО

8

ЗА

9

НЕ

10

РЕС

11

ЧИ

12

ТЕ

13

ВА

КЛЮЧ

13.11.18

«Золотые мысли»

№ уравнения

2

8

1

3

5

10

7

,

4

9

6

7

Ян Амос Коменский (1592-1670),

чешский педагог, писатель.

13.11.18

Домашнее задание

• Решите уравнение х 2 +6х-16=0 по формуле, выделением квадрата двучлена и графическим методом

• Решите уравнение 3х 2 +5х+2=0 пятью способами.

• Решите уравнение (х 2 -х) 2 — 14(х 2 -х)+24=0 методом введения новой переменной.

13.11.18