Понятие цилиндра.
11 класс
Цилиндры вокруг нас.
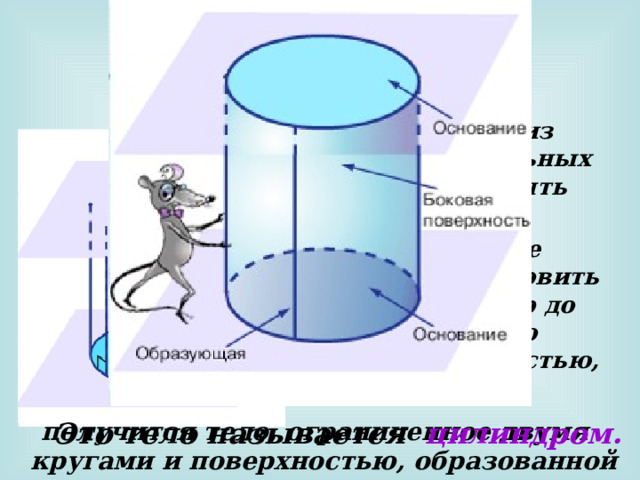
Цилиндрическая поверхность.
Если в одной из двух параллельных плоскостей взять окружность,
и из каждой ее точки восстановить перпендикуляр до пересечения со второй плоскостью, то
получится тело, ограниченное двумя кругами и поверхностью, образованной из перпендикуляров.
Это тело называется цилиндром.

Точное название определенного выше тела – прямой круговой цилиндр.
Вообще, цилиндр возникает при пересечении цилиндрической поверхности, образованной множеством параллельных прямых, проведенных через каждую точку замкнутой кривой линии, и двух параллельных плоскостей.
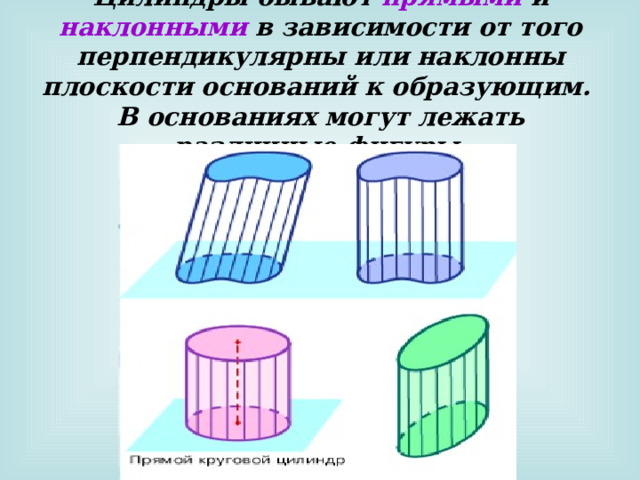
Цилиндры бывают прямыми и наклонными в зависимости от того перпендикулярны или наклонны плоскости оснований к образующим. В основаниях могут лежать различные фигуры.
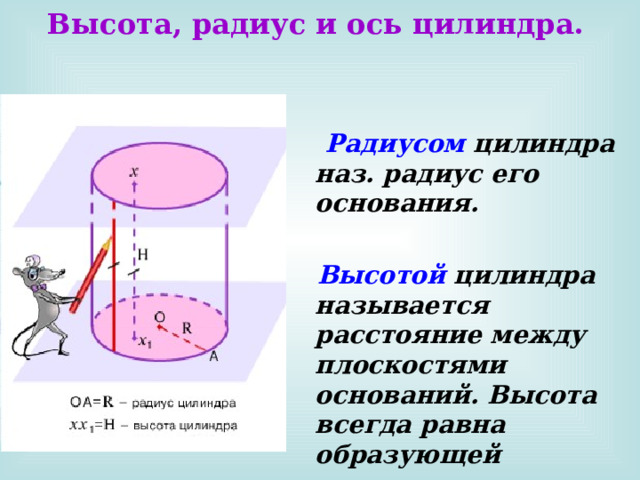
Высота, радиус и ось цилиндра.
Радиусом цилиндра наз. радиус его основания.
Высотой цилиндра называется расстояние между плоскостями оснований. Высота всегда равна образующей

Вспомните формулу нахождения площади круга и найдите площадь основания цилиндра , радиус которого равен 2.
4
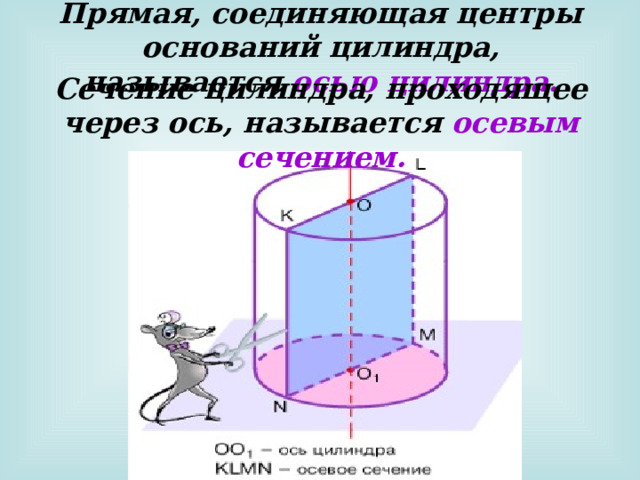
Прямая, соединяющая центры оснований цилиндра, называется осью цилиндра.
Сечение цилиндра, проходящее через ось, называется осевым сечением.
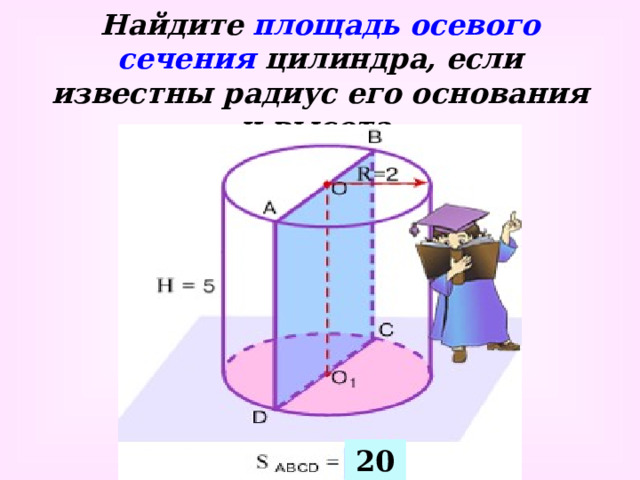
Найдите площадь осевого сечения цилиндра, если известны радиус его основания и высота.
20
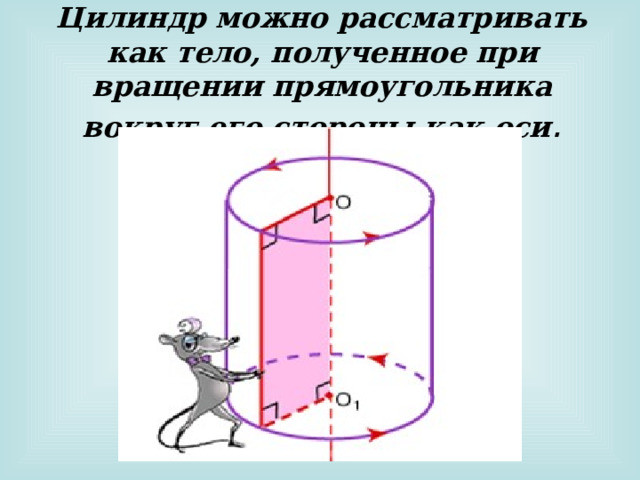
Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг его стороны как оси .
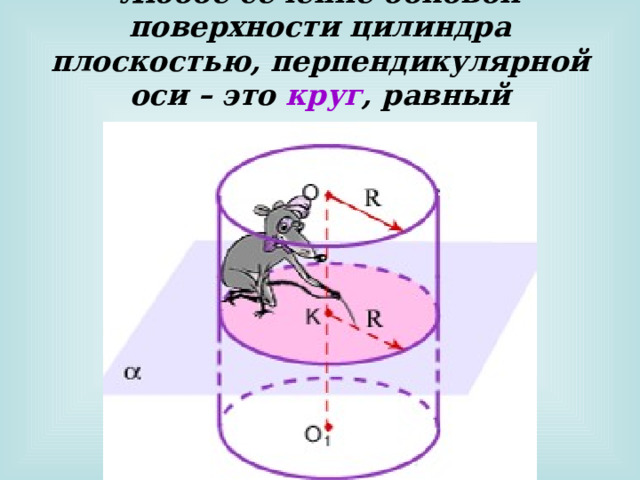
Любое сечение боковой поверхности цилиндра плоскостью, перпендикулярной оси – это круг , равный основанию.
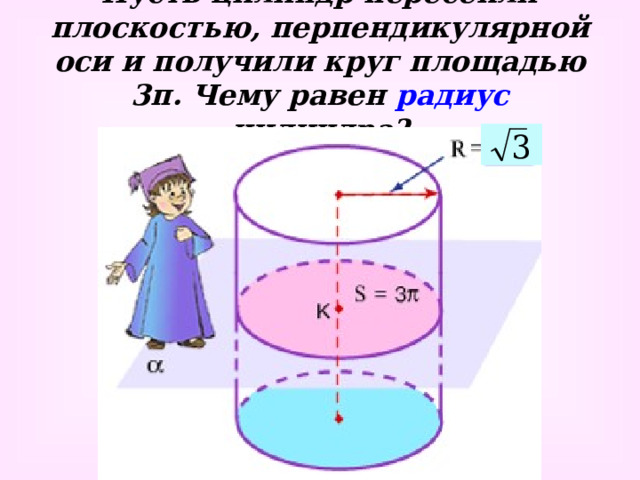
Пусть цилиндр пересекли плоскостью, перпендикулярной оси и получили круг площадью 3 π . Чему равен радиус цилиндра?

Задача.
Высота цилиндра 7 см, а радиус основания 5 см. В цилиндре расположена трапеция так, что все ее вершины находятся на окружностях оснований цилиндра. Найти площадь трапеции и угол между основанием и плоскостью трапеции, если параллельные стороны трапеции равны 6см и 8 см.
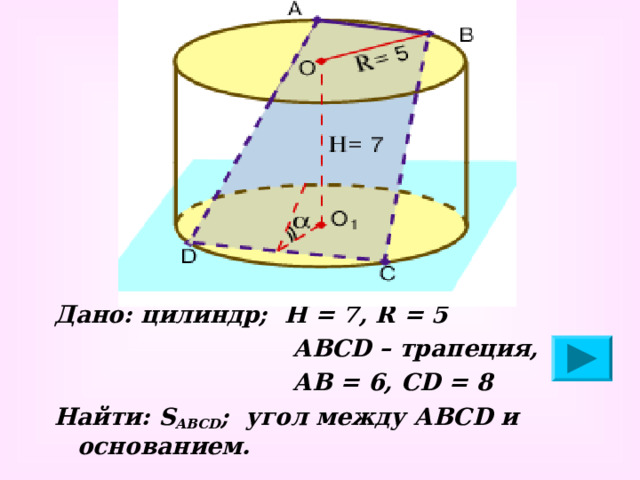
Дано: цилиндр; Н = 7, R = 5
АВС D – трапеция,
АВ = 6, С D = 8
Найти: S ABCD ; угол между АВС D и основанием.
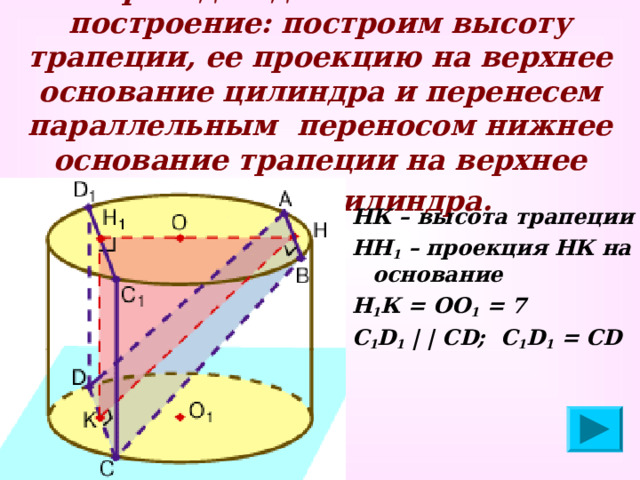
Проведем дополнительное построение: построим высоту трапеции, ее проекцию на верхнее основание цилиндра и перенесем параллельным переносом нижнее основание трапеции на верхнее основание цилиндра.
НК – высота трапеции
НН 1 – проекция НК на основание
Н 1 К = ОО 1 = 7
С 1 D 1 | | С D ; С 1 D 1 = CD
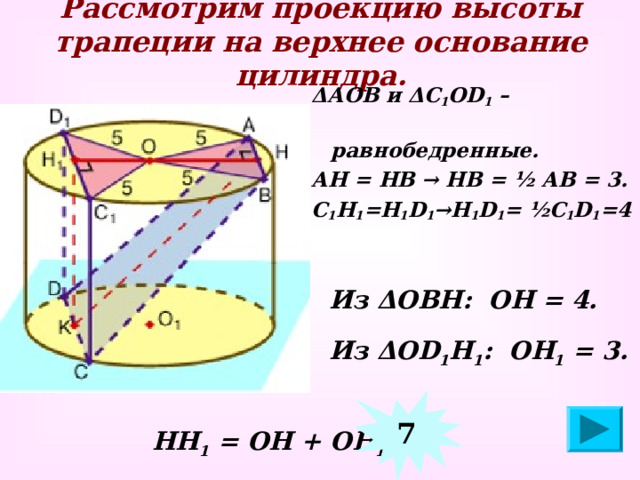
Рассмотрим проекцию высоты трапеции на верхнее основание цилиндра.
Δ АОВ и Δ С 1 О D 1 –
равнобедренные.
АН = НВ → НВ = ½ АВ = 3.
С 1 Н 1 =Н 1 D 1 → Н 1 D 1 = ½С 1 D 1 =4
Из Δ ОВН: ОН = 4.
Из Δ О D 1 Н 1 : ОН 1 = 3 .
7
НН 1 = ОН + ОН 1 =
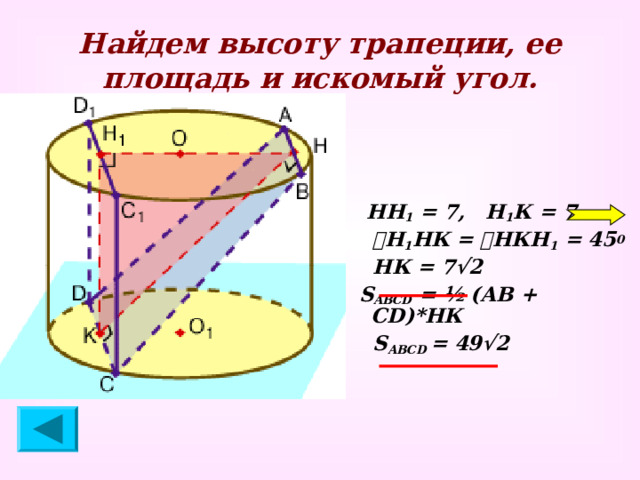
Найдем высоту трапеции, ее площадь и искомый угол.
НН 1 = 7, Н 1 К = 7
ے Н 1 НК = ے НКН 1 = 45 0
НК = 7√2
S ABCD = ½ (АВ + С D )*НК
S АВС D = 49√2
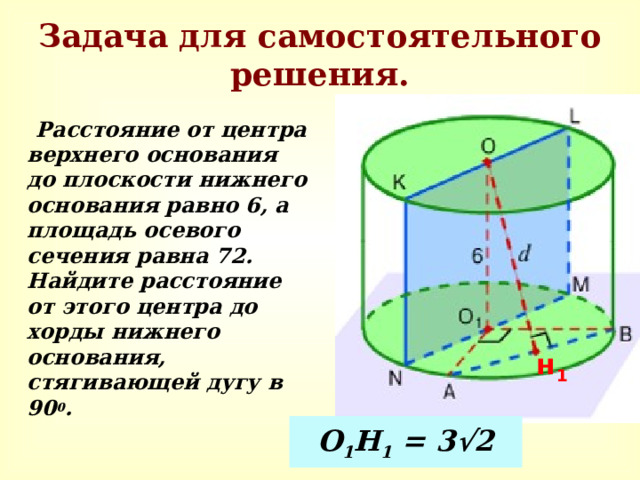
Задача для самостоятельного решения.
Расстояние от центра верхнего основания до плоскости нижнего основания равно 6, а площадь осевого сечения равна 72. Найдите расстояние от этого центра до хорды нижнего основания, стягивающей дугу в 90 0 .
н 1
О 1 Н 1 = 3 √2

Домашнее задание:
П. 53, 54
№№ 523, 525, 529.